江西省2024年初中学业水平考试样卷试题卷(一)1数学

江西省2024年初中学业水平考试样卷试题卷(一)1数学试卷答案,试题汇目前收集并整理关于江西省2024年初中学业水平考试样卷试题卷(一)1数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

江西省2024年初中学业水平考试样卷试题卷(一)1数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

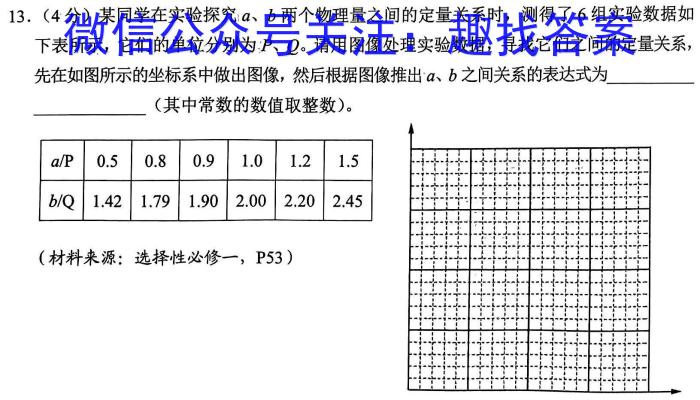
13.(4分)某同学在实验探究a、b两个物理量之间的定量关系时,测得了6组实验数据如下表所示,它们的单位分别为P、O。请用图像处理实验数据,寻找它们之间的定量关系,先在如图所示的坐标系中做出图像,然后根据图像推出a、b之间关系的表达式为(其中常数的数值取整数)。(材料来源:选择性必修一,P53)

分析（Ⅰ）把a_n=S_n-S_n-1（n≥2）代入2a_nS_n-a_n²=1，整理后即可证明{S_n²}是等差数列，求其通项公式后再由a_n=S_n-S_n-1（n≥2）求数列{a_n}的通项公式；
（Ⅱ）把S_n²=n代入S_n²x^n-1，对x分类后借助于等比数列的前n项和求得数列{S_n²x^n-1}的前n项和T_n．

解答（Ⅰ）证明：∵2a_nS_n-a_n²=1，
∴当n≥2时，2（S_n-S_n-1）S_n-$（{S}_{n}-{S}_{n-1}）^{2}=1$，
整理得，${{S}_{n}}^{2}-{{S}_{n-1}}^{2}=1$（n≥2），
又${{S}_{1}}^{2}$=1，
∴数列{S_n²}为首项和公差都是1的等差数列．
∴${{S}_{n}}^{2}=n$，
又S_n＞0，∴S_n=$\sqrt{n}$．
∴n≥2时，a_n=S_n-S_n-1=$\sqrt{n}-\sqrt{n-1}$，又a₁=S₁=1适合此式．
∴数列{a_n}的通项公式为a_n=$\sqrt{n}-\sqrt{n-1}$；
（Ⅱ）解：S_n²x^n-1=n•x^n-1．
当x=0时，T_n=0；
当x=1时，T_n=1+2+…+n=$\frac{n（n+1）}{2}$；
当x≠0且x≠1时，
T_n=1•x⁰+2•x¹+3•x²+…+n•x^n-1．
$x{T}_{n}=1•{x}^{1}+2•{x}^{2}+3•{x}^{3}+…+（n-1）{x}^{n-1}+n{x}^{n}$．
两式作差得：$（1-x）{T}_{n}=1+x+{x}^{2}+…+{x}^{n-1}-n{x}^{n}$=$\frac{1-{x}^{n}}{1-x}-n{x}^{n}$．
∴${T}_{n}=\frac{1-{x}^{n}}{（1-x）^{2}}-\frac{n{x}^{n}}{1-x}$．
综上，当x=0时，T_n=0；
当x=1时，T_n=$\frac{n（n+1）}{2}$；
当x≠0且x≠1时，${T}_{n}=\frac{1-{x}^{n}}{（1-x）^{2}}-\frac{n{x}^{n}}{1-x}$．

点评本题考查数列递推式，考查了等差关系的确定，训练了等比数列前n项和的求法，体现了分类讨论的数学思想方法，是中档题．

【江西省2024年初中学业水平考试样卷试题卷(一)1数学】相关文章：