安徽中考2024年九年级试题卷(五)5数学

安徽中考2024年九年级试题卷(五)5数学试卷答案,试题汇目前收集并整理关于安徽中考2024年九年级试题卷(五)5数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

安徽中考2024年九年级试题卷(五)5数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

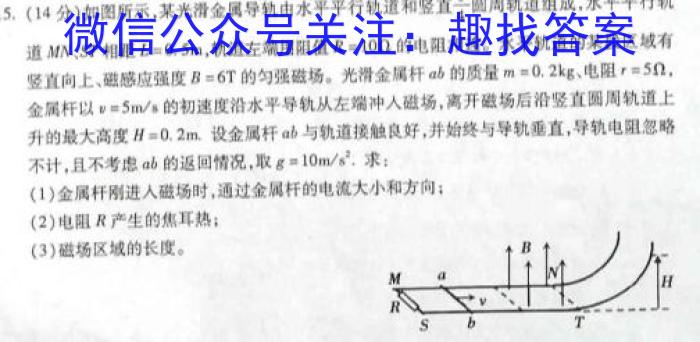
15.(14分)如图所示,某光滑金属导轨由水平平行轨道和竖直圆周轨道组成,水平平行轨道N、ST相距L=0.5m,,轨道左端用阻值R=10Ω的电阻相连。水平轨道的某段区域有竖直向上、磁感应强度,B=6T的匀强磁场。光滑金属杆,ab的质量m=0.2kg、、电阻r=5Ω,金属杆以v=5m/s的初速度沿水平导轨从左端冲人磁场,离开磁场后沿竖直圆周轨道上升的最大高度H=0.2m.设金属杆ab与轨道接触良好,并始终与导轨垂直,导轨电阻忽略不计,且不考虑ab的返回情况,取g=10m/s^2.求:(1)金属杆刚进入磁场时,通过金属杆的电流大小和方向;(2)电阻产生的焦耳热;(3)磁场区域的长度。

分析（1）记“恰有2人申请A大学或B大学”为事件M，利用n次独立重复试验中事件A恰好发生中k次的概率计算公式能求出恰有2人申请A大学或B大学的概率．
（2）由题意X的所有可能取值为0，1，2，3，4，且X～B（4，$\frac{1}{3}$），由此能求出X的分布列和E（X）．

解答解：（1）记“恰有2人申请A大学或B大学”为事件M，
则P（M）=${C}_{4}^{2}（\frac{2}{3}）^{2}（\frac{1}{3}）^{2}$=$\frac{8}{27}$，
∴恰有2人申请A大学或B大学的概率为$\frac{8}{27}$．
（2）由题意X的所有可能取值为0，1，2，3，4，且X～B（4，$\frac{1}{3}$），
P（X=0）=${C}_{4}^{0}（\frac{2}{3}）^{4}$=$\frac{16}{81}$，
P（X=1）=${C}_{4}^{1}（\frac{1}{3}）（\frac{2}{3}）^{3}$=$\frac{32}{81}$，
P（X=2）=${C}_{4}^{2}（\frac{1}{3}）^{2}（\frac{2}{3}）^{2}$=$\frac{24}{81}$，
P（X=3）=${C}_{4}^{3}（\frac{1}{3}）^{3}（\frac{2}{3}）$=$\frac{8}{81}$，
P（X=4）=${C}_{4}^{4}（\frac{1}{3}）^{4}$=$\frac{1}{81}$，
∴X的分布列为： X 0 1 2 3 4 P $\frac{16}{81}$ $\frac{32}{81}$ $\frac{24}{81}$ $\frac{8}{81}$ $\frac{1}{81}$E（X）=4×$\frac{1}{3}$=$\frac{4}{3}$．

点评本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意二项分布的性质的合理运用．

【安徽中考2024年九年级试题卷(五)5数学】相关文章：