2024年高考冲刺模拟试卷(七)7数学

2024年高考冲刺模拟试卷(七)7数学试卷答案,试题汇目前收集并整理关于2024年高考冲刺模拟试卷(七)7数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2024年高考冲刺模拟试卷(七)7数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

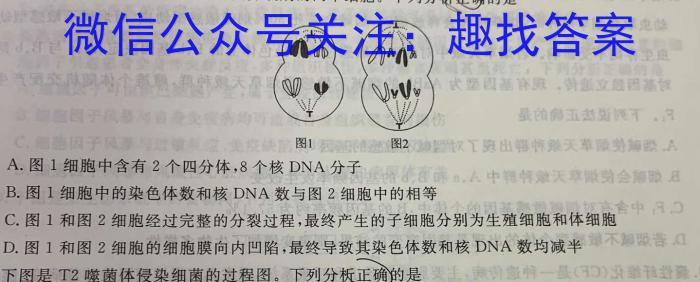
C.图1A.图1细胞中含有2个四分体,8个核DNA分子B.图1细胞中的染色体数和核DNA数与图2细胞中的相等C.图1和图2细胞经过完整的分裂过程,最终产生的子细胞分别为生殖细胞和体细胞D.图1和图2细胞的细胞膜向内凹陷,最终导致其染色体数和核DNA数均减半

分析根据函数为奇函数可得-f（-2m-2）=f（2m+2），利用单调性可得cos²θ+2msinθ＜2m+2恒成立．利用换元法令t=sinθ∈[0，1]，真理为t²-2mt+2m+1＞0在t∈[0，1]恒成立．对二次函数的对称轴分别讨论，求出区间内的最小值即可．

解答解：由条件可得：f（cos²θ+2msinθ）＜-f（-2m-2）
由于函数是定义在R上的单调递增奇函数，
∴cos²θ+2msinθ＜2m+2恒成立．
设t=sinθ∈[0，1]，
∴t²-2mt+2m+1＞0在t∈[0，1]恒成立．
只要g（t）=t²-2mt+2m+1在[0，1]的最小值大于0即可．
（1）当m＜0时，最小值为g（0）=2m+1＞0，所以可得：0＞m＞-$\frac{1}{2}$
（2）当0≤m≤1时，最小值为g（m）=-m²+2m+1＞0，所以可得：0≤m≤1
（3）当m＞1时，最小值为g（1）=2＞0恒成立，得：m＞1，（13分）
综之：m＞-$\frac{1}{2}$，
故答案为m＞-$\frac{1}{2}$．

点评考查了奇函数的性质和应用，二次函数闭区间上最小值的求法．属于基础题型，应熟练掌握．

【2024年高考冲刺模拟试卷(七)7数学】相关文章：