2024年陕西省初中学业水平适应性联考(二)2数学

2024年陕西省初中学业水平适应性联考(二)2数学试卷答案,试题汇目前收集并整理关于2024年陕西省初中学业水平适应性联考(二)2数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2024年陕西省初中学业水平适应性联考(二)2数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

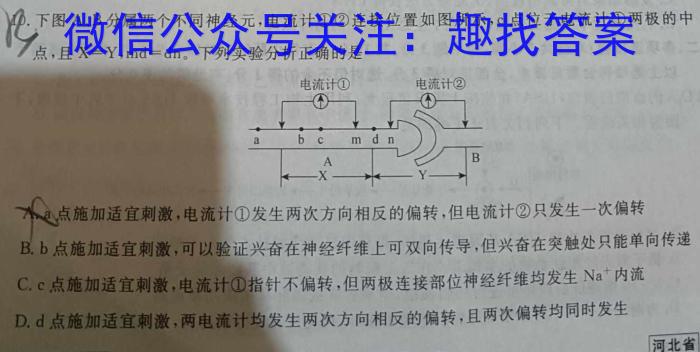
.下图A、B分属两个不同神经元,电流计①②连接位置如图所示,c点位于电流计①两极的中点,且X=Y,md=dn。,下列实验分析正确的是点点施施加适宜刺激,电流计①发生两次方向相反的偏转,但电流计②只发生一次偏转B.b点施加适宜刺激,可以验证兴奋在神经纤维上可双向传导,但兴奋在突触处只能单向传递C.c点施加适宜刺激,电流计①指针不偏转,但两极连接部位神经纤维均发生Na^+D.d点施加适宜刺激,两电流计均发生两次方向相反的偏转,且两次偏转均同时发生河北省

分析（1）当$θ=\frac{π}{6}$时可得$\overrightarrow{a}$=$（1，\frac{1}{2}）$，由向量的运算可得；
（2）由向量平行可得$sinθ=\frac{1}{2}$，由同角三角函数基本关系可得$cosθ=\frac{{\sqrt{3}}}{2}$，代入两角和的正弦公式可得．

解答解：（1）∵$θ=\frac{π}{6}$，∴$\overrightarrow{a}$=$（1，\frac{1}{2}）$，
∴向量2$\overrightarrow{a}$+$\overrightarrow{b}$=$2（1，\frac{1}{2}）+（2，1）=（4，2）$；
（2）∵$\overrightarrow{a}$∥$\overrightarrow{b}$，∴$sinθ=\frac{1}{2}$，
又∵$θ∈（0，\frac{π}{2}）$，∴$cosθ=\frac{{\sqrt{3}}}{2}$，
∴$sin（θ+\frac{π}{4}）=sinθcos\frac{π}{4}+cosθsin\frac{π}{4}=\frac{{\sqrt{2}+\sqrt{6}}}{4}$

点评本题考查两角和与差的三角函数公式，涉及向量的运算和同角三角函数基本关系，属基础题．

【2024年陕西省初中学业水平适应性联考(二)2数学】相关文章：