2023-2024学年吉林省高二4月联考(24-416B)数学

2023-2024学年吉林省高二4月联考(24-416B)数学试卷答案,试题汇目前收集并整理关于2023-2024学年吉林省高二4月联考(24-416B)数学得系列试题及其答案，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

2023-2024学年吉林省高二4月联考(24-416B)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

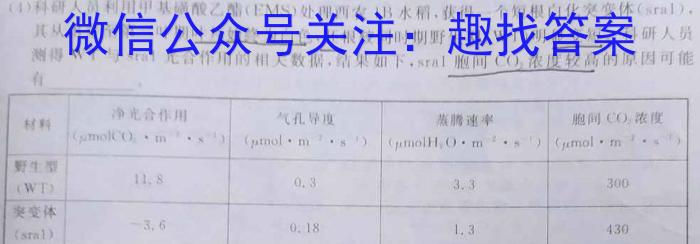
(1)科研人员利用甲基磺酸乙酯(EMS)处理西农1B水稻,获得一个短根白化突变体其从出身至第三叶期叶片始为白色,胚根较同时期野生型(W个)明显变短科研人员测得WT与sral光合作用的相关数据,结果如下,sral胞间CO浓度较高的原因可能有

分析由根式内部的代数式大于等于0，0指数幂的底数不等于0联立不等式组求解．

解答解：由$\left\{\begin{array}{l}{x+1≥0}\\{2-x≠0}\end{array}\right.$，解得：x≥-1，且x≠2．
∴函数$f（x）=\sqrt{x+1}+{（2-x）^0}$的定义域为{x|x≥-1，且x≠2}．
故答案为：{x|x≥-1，且x≠2}．

点评本题考查函数的定义域及其求法，是基础的计算题．

【2023-2024学年吉林省高二4月联考(24-416B)数学】相关文章：